如果只沉迷于无意义的炼丹，我们的编程水平会不可否认的越来越差的。

作为每一个torch模型的base class，

LayerNorm & BatchNorm & GroupNorm

这些都是深度学习中常用的归一化方式，他们都是将输入归一化到均值为0和方差为1的分布中，来防止梯度消失和爆炸，并提高模型的泛化能力,那么它们的区别是什么呢，我们在使用时候又该如何去区分呢

BatchNorm

常见的情况是这样的：在CNN中，卷积层后面会跟一个BatchNorm层，（因为归一化之后的数据大多都为0.几了，如果不进行归一化，1.几这样连续地乘上几次就爆炸了，同样如果是0.0000 连续地乘上几次梯度就消失不见了）防止梯度的消失和爆炸，从而提高模型的稳定性。以下面的图示为例：

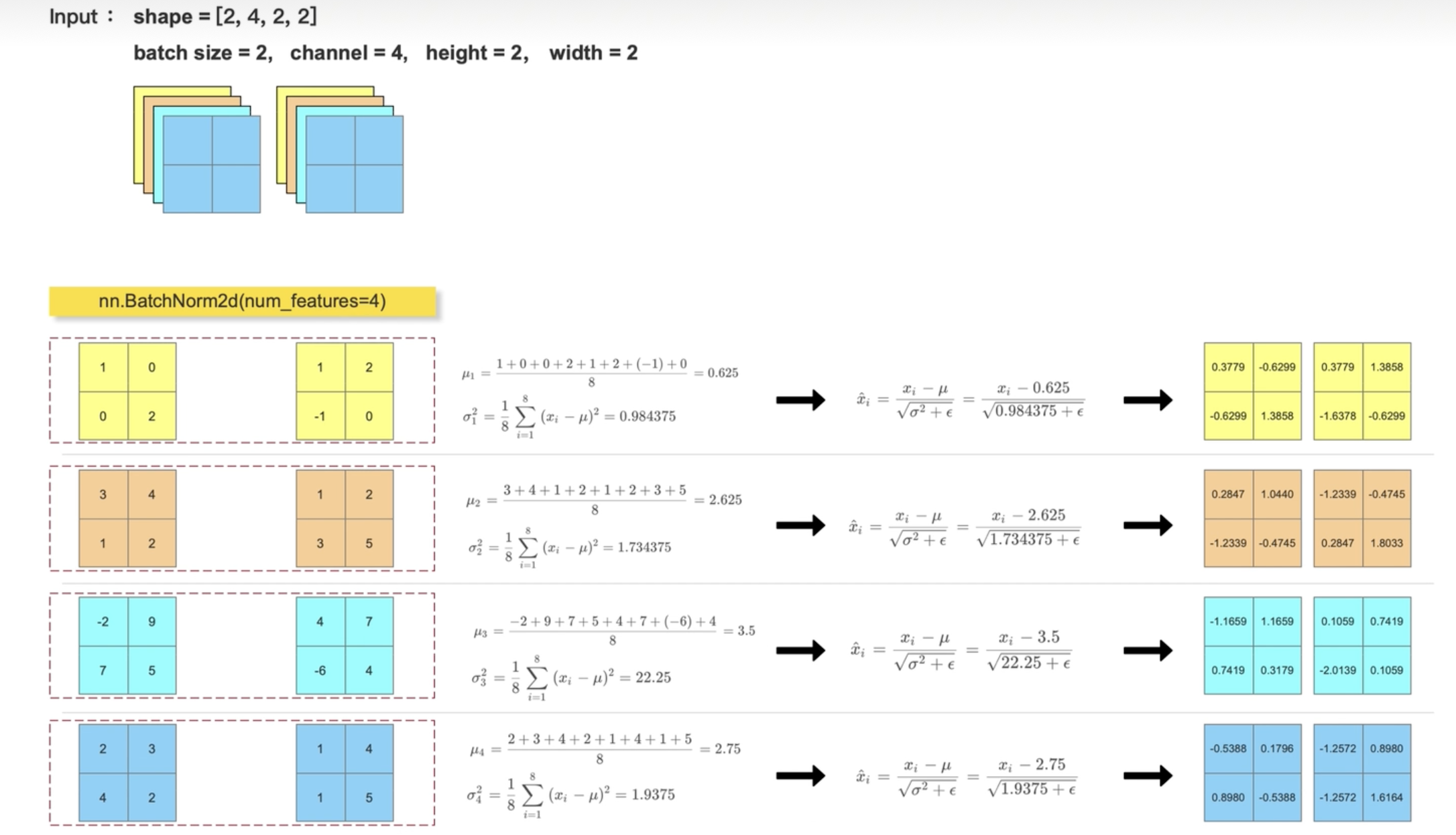
在上图的示例中，我们使用的是nn.BatchNorm2d(num_features=4)。这里输入的参数是4表示的是输入的通道数量是4.这里比较反直觉的是，对于(2,4,2,2)形状的Tensor，其做归一化的维度是channels维度，如果这个过程从0开始手写是这样的：

for i in range(feature_array.shape[0]):
    channel = feature_array[:,i,:,:]
    mean = channel.mean()
    var = channel.var()

    feature_array[:,i,:,:] = (channel - mean)/np.sqrt(var + 1e-5)

如果使用torch的框架是这样的：

import torch.nn as nn
bn_out = nn.BatchNorm2d(num_features = 4,eps=1e-5)(feature_tensor)

LayerNorm

layerNorm操作更常见是在Transformer的结构中，一般输入的尺寸为(batch_size,token_num,dim),然后会在最后一个维度(每个tokeb的维度)去做归一化，一般是使用nn.LayerNorm(dim)来进行层归一化的操作。

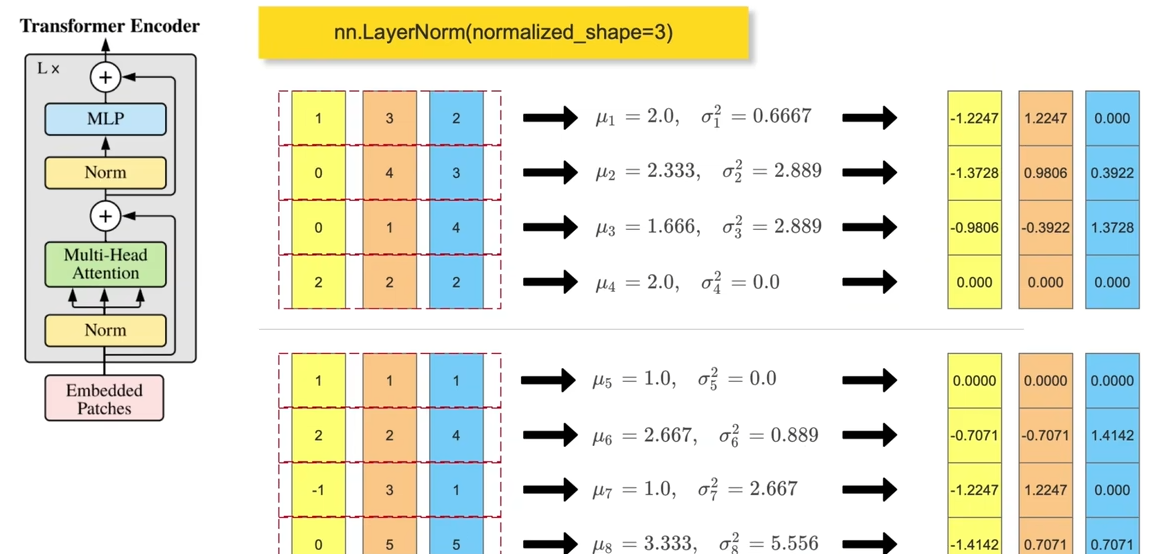
GroupNorm

一般，当batchsize过大或者过小时候都不适合BatchNorm,Batchsize过大时候，BN会将所有的数据归一化到相同的均值和方差，而batchsize过小时候，BN可能无法有效学习数据的统计信息。（GroupNorm在当前的大模型用的比较火

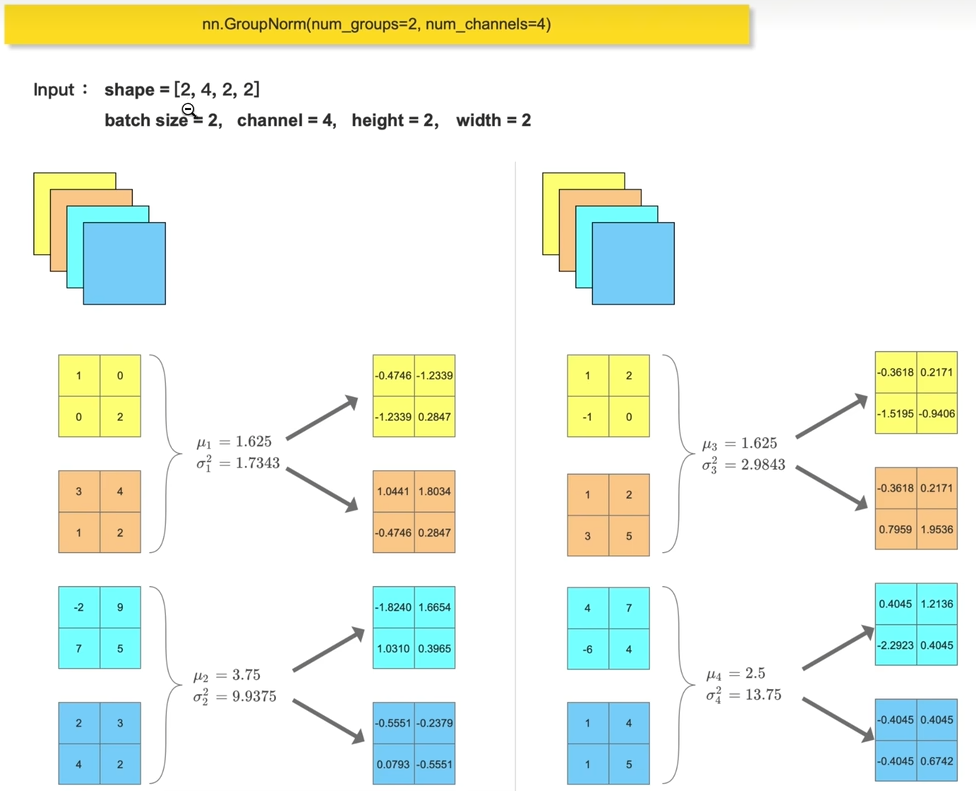
上图是在nn.GroupNorm(num_groups=2,num_channels=4)的情况下进行的，也即图像有四个通道，然后我们将四个通道分成两个组。

计算图の概念

针对于叶子节点：

• 一个错误例子示范

a = Variable(torch.rand(1, 4), requires_grad=True)
b = a**2
c = b*2

d = c.mean()
e = c.sum()


d.backward()

# RuntimeError: Trying to backward through the graph a second time
e.backward()

在执行e.backward()时候会报错，提示在试图通过这个计算图传播两次

我们将上述代码中的操作以计算图的形式进行可视化：

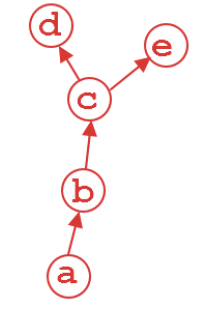
在该图中，叶子节点为a

• 我们只需要将代码改成这样即可：

a = Variable(torch.rand(1, 4), requires_grad=True)
b = a**2
c = b*2

d = c.mean()
e = c.sum()


d.backward(retain_graph=True)  # 保留计算图

e.backward()  # 再次对e进行梯度计算，梯度会累加上去

此时，来梳理下其具体的计算过程：

我们可以看出，d和e都是关于a的函数，经过backward操作，a的梯度是会累加起来的，例如下面的这段代码：

a # 此时a的值为tensor([[0.3904, 0.6009, 0.2566, 0.7936]], requires_grad=True)

a.grad # 代表的是变量 a 相对于某个标量输出（在这里是 d 和 e）的梯度 ，在执行完`e.backward()`操作之后，输出的是e的梯度
# tensor([[1.9522, 3.0045, 1.2829, 3.9682]])

5*a
# tensor([[1.9522, 3.0045, 1.2829, 3.9682]], grad_fn=<MulBackward0>)

针对于非叶子节点：

如果访问梯度的节点为非叶子节点：

a = Variable(torch.rand(1, 4), requires_grad=True)
b = a**2
c = b*2

d = c.mean()

d.backward()
b.grad

这样会爆出下面的错误：

/tmp/ipykernel_10679/3238518479.py:1: UserWarning: The .grad attribute of a Tensor that is not a leaf Tensor is being accessed. Its .grad attribute won't be populated during autograd.backward(). If you indeed want the .grad field to be populated for a non-leaf Tensor, use .retain_grad() on the non-leaf Tensor. If you access the non-leaf Tensor by mistake, make sure you access the leaf Tensor instead. See github.com/pytorch/pytorch/pull/30531 for more informations. (Triggered internally at aten/src/ATen/core/TensorBody.h:489.)
  b.grad

此时，可以试图去访问下b，我们得到b为tensor([[0.8851, 0.0177, 0.8735, 0.3523]], grad_fn=<PowBackward0>) 我们查看下b的is_leaf属性，果不其然，为False

此时，我们只需要加上一行变成这样：

a = Variable(torch.rand(1, 4), requires_grad=True)
b = a**2
b.retain_grad()
c = b*2

d = c.mean()
d.backward()
b.grad

可以得到b.grad的值为tensor([[0.5000, 0.5000, 0.5000, 0.5000]])

根据这里简单的推导，我们很轻松地发现这是d对于b的导数，结果为$\frac{1}{2}$

深度网络实践中的计算图

• nn中间层的weights

class MLP(nn.Module):
    def __init__(self):
        super(MLP, self).__init__()
        self.fc1 = nn.Linear(28*28, 512)
        self.fc2 = nn.Linear(512, 512)
        self.fc3 = nn.Linear(512, 10)

    def forward(self, x):
        x = nn.Flatten(x)
        x = self.fc3(nn.ReLU(self.fc2(nn.ReLU(self.fc1(x)))))
        return x
mlp = MLP()
mlp.fc1.weight.is_leaf
True
mlp.fc2.weight.is_leaf
True
mlp.fc3.weight.is_leaf
True

• 计算图总结

• 反向传播，链式法则，内部非叶子节点（non-leaf node，哪怕 requires_grad 为 true，且其存在 grad_fn）也是会算梯度的，只是用完就置空了，
  • 因此如果相查看内部非叶子节点的 grad，需要 retain_graph 保留在计算图中;
• 深度神经网络中的中间层 layer 的参数（weights & bias）它们是内部节点呢，还是叶子节点呢？
  • 是叶子节点；
• 不要轻易地关闭 warnings，有助于排查/定位问题；
  • warnings 不会导致程序 dump，但不推荐，因为有可能导致程序的运行不符合预期；
  • 对于自己写的代码，出于健壮性或者可快速定位问题的考虑，也可以尝试多写 warnings

参考资料

Pytorch官方Docs

BilibiliUp主：Enzo_Mi

BilibiliUp主：五道口纳什