Cai-Mingshuo

Cai-Mingshuo

Go forward and don't look back!

Diffusion入门知识1—初识VAE

1 minute read

Published:

这篇博客介绍了我在入门diffusion时入门所学到的一些生成模型的的笔记

VAE

AE Auto-Encoder

Auto是自己训练自己的意思，由encoder和decoder组成，重建图像和原始图像之间的重建损失来进行优化，AE一般都是用于降维的，一般用于压缩重构；VAE则是用来做generative,做图像生成。

Alt text

VAE Variational Auto-Encoder

简介

变分自编码器，Variation指的是分布的意思，意思是不在把分布映射到固定的变量上，而是映射到一个分布上(例如高斯分布模型)。

这里的conv和deconv有点意思

VAE网络结构

  • Encoder&Decoder
    • Encoder: $q(z\vert x)$(神经网络的参数为$\phi$) => $q_{\phi}(z\vert x)$
    • Decoder： $p(x\vert z)$(神经网络的参数为$\theta$) = > $p_{\theta}(x\vert z)$
  • latent space
    • 编码器的输出：是两个向量，一个是均值向量$\mu$,一个是标准差向量$\sigma$,他们长度相同，一起定义了输入数据在latent space中的represention

VAE损失函数

\[{\mathcal L}(\theta,\phi;\mathbf{x},\mathbf{z})=\underbrace{\mathbb{E}_{q_{\phi}(z\vert x)}\left[\log p_{\theta}(x\vert z)\right]}_{\text{reconstruction loss}}-\underbrace{D_{KL}\left(q_{\phi}(z\vert x)\vert p(z)\right)}_{\text{stay close to Normal}(0,1)}\]

直观的理解

一般来说 我们通过观测数据来获得对数据的见解或者知识，比如看到一个图片就可以知道其是哪个类别(我们称之为推理”);我们可以通过采样来获得$\chi\sim\mathcal{P}(X)$，然后可以通过条件概率$z\thicksim p(z\vert x)$来对隐变量$z$进行采样从而可以完成推理的过程 贝叶斯推理过程（即为$z$）为

\[p(z\vert x)=\frac{p(x\vert z)p(z)}{p_{\theta}(x)}=\frac{p(x\vert z)p(z)}{\int_{z}p_{\theta}(x,z)dz}\]

该式得到的是一种真实的概率分布，但是这个尤其是$p_{\theta}$比较难算，则使用一组近似的过程去近似这个过程(我们称之为“变分”)或者另一种方法是模特卡罗采样,下面是对这个内容的举例说明。

Example 1

隐变量z的分布为

\[z\sim p(z)=\begin{cases}e^{-z},z\geq0\\0&,z<0\end{cases}=e^{-z}I(z\geq0)\]

通过均值这个参数和隐变量去关联起来

\[x-p(x\vert z)=N(x,\mu=z,\sigma=1)=\frac1{\sqrt{2\pi}}e^{(-\frac12(x-z)^2)}\]

其联合概率分布为

\[p(x,z)=p(x\vert z)p(z)=\frac{1}{\sqrt{2\pi}}e^{(-\frac{1}{2}(x-z)^2)}e^{-z}I(z\geq0)\]

边缘概率密度(在隐空间内进行积分)为

\[p(x)=\int_0^\infty p(x,z)\mathrm{~}dz=\int_0^\infty e^{-z}\frac1{\sqrt{2\pi}}e^{(-\frac12(x-z)^2)}\mathrm{~}dz\]

可以看出这个积分十分地复杂，无法进行计算。

Example 2

在贝叶斯公式中，我们可以看出，后验概率$p(z\vert x)$是正比于联合概率分布$P(x,z)$有

\[p(x,z)=p(x\vert z)p(z)=\frac{1}{\sqrt{2\pi}}e^{(-\frac{1}{2}(x-z)^{2})}e^{-z}I(z\geq0)\] \[\begin{aligned} &p(z|x)\sim p(x,z)=p(x|z)p(z)=\frac{1}{\sqrt{2\pi}}e^{(-\frac{1}{2}(x-z)^{2})}e^{-z}I(z\geq0) \\ &=\frac{1}{\sqrt{2\pi}}e^{(-\frac{1}{2}z^{2}+(x-1)z-\frac{1}{2}x^{2})}I(z\geq0) \\ &=\frac{1}{\sqrt{2\pi}}e^{(-\frac{1}{2}(z-(x-1))^{2}+\frac{1}{2}(x-1)^{2}-\frac{1}{2}x^{2})}I(z\geq0) \\ &=\frac{1}{\sqrt{2\pi}}e^{(\frac{1}{2}(x-1)^{2}-\frac{1}{2}x^{2})}e^{(-\frac{1}{2}(z-(x-1))^{2})}I(z\geq0) \\ &\sim\frac{1}{\sqrt{2\pi}}e^{(-\frac{1}{2}(z-(x-1))^{2})}I(z\geq0) \end{aligned}\]

经过一系列如上的推导，最终得到后验概率为$p(z\vert x){\sim}\frac1{\sqrt{2\pi}}e^{(-\frac12(z-(x-1))^2)}I(z\geq0)$说明$p(z\vert x)$在$z\geq0$时正比于均值为1的高斯分布

Example 3

针对不同的概率值，其观测的边缘概率值是不同的

在这三个例子下，我们看到了后验概率$p_{\theta}(z\vert x)$与其他变量有很多的关系，这里引入$q_{\phi}(z)$来进行对其进行逼近

\[\begin{split} KL\left[q_\phi(z)\vert p_\theta(z\vert x)\right]&=-\sum_zq_\phi(z)\log \frac{p_\theta(z\vert x)}{q_\phi(z)}\\ &=-\underset{z}{\sum} q_{\phi}(z) \log \bigg( \frac{p_{\theta}(x,z)}{q_{\phi}(z)} \cdot \frac{1}{p_{\theta}(x)} \bigg) \\ &= -\underset{z}{\sum} q_{\phi}(z) \bigg( \log\frac{p_{\theta}(x,z)}{q_{\phi}(z)} - \log p_{\theta}(x) \bigg) \\ &= -\underset{z}{\sum} q_{\phi}(z) \log \frac{p_{\theta}(x,z)}{q_{\phi}(z)} + \underset{z}{\sum} q_{\phi}(z) \log p_{\theta}(x)\\ &== -\underset{z}{\sum} q_{\phi}(z) \log \frac{p_{\theta}(x,z)}{q_{\phi}(z)} + \log p_{\theta}(x) \end{split}\]

从一个比较直观的角度去理解VAE

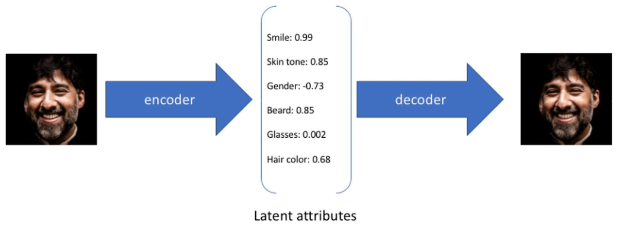
Alt text

  • 自己训练自己的目的是可以在编码器中得到一个维度远远小于原图的隐变量(latent/smaller/compressed representation)，也即一组对图片的压缩表示。
  • AE的重点是针对于隐变量$(z)$去建模
    • 隐变量(Latent variables)是指不可以被直接观察到的变量：例如对健康，智商的评估；可以通过一组可以观测的指标来infer(推断)
    • LDM: Latent Diffusion Model
  • AE关心的是z(latent vectors/variables),前半部分(encoder)，其decoder只是用于确保可以学到一个很好的encoder而已。
  • 而VAE只是关心的是生成的过程。

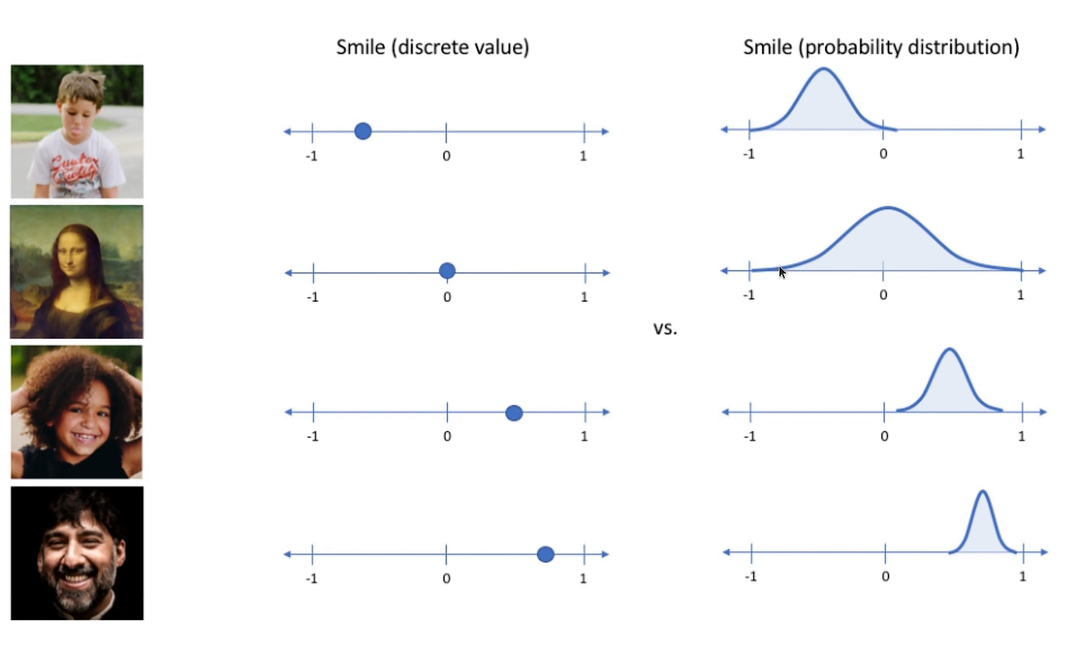
Alt text

  • 可以使用高斯分布的随机变量来表示这些属性(以上图中的smile)为例，那么这些属性就可以从数字变成单一分布的概率分布。

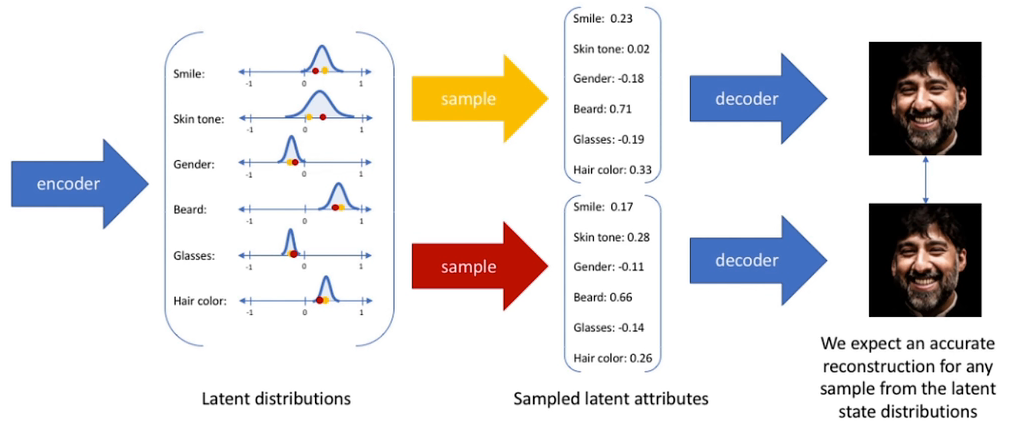
Alt text

  • 通过训练，这里得到的这些图片是原始图片的压缩表示，简单来说为在隐空间中获得采样，通过解码器获取新的图片

VAE初步总结

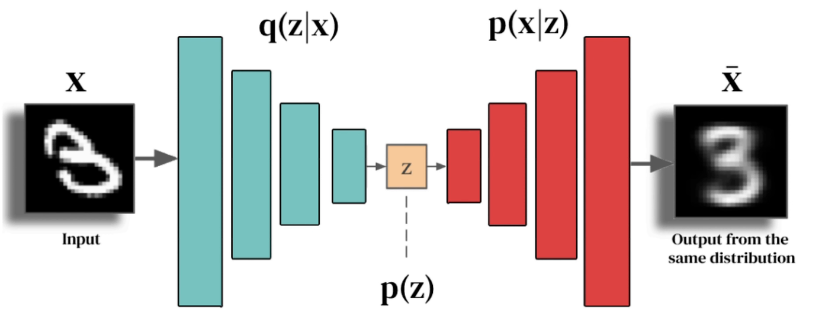
Alt text

  • input: $x$ ,hidden: $\mu$ , $\sigma$ ,output $\tilde{x}$.
    • $x$ : data，可观测的；latent variable models假设的是，latent space中的$z$导致了$x$
    • 概率图的角度就是 $z->x(generative models的generation process)$
      • Encoder就是$q_{\phi}(z\vert x),x->z$
      • latent distribution $z=\mu+\sigma\odot\epsilon $
      • Decoder就是$p_{\theta}(x\vert z),z\rightarrow{\tilde{x}}$
      • $q_{\phi}$和$p_{\theta}$是非常经典的一对

参考资料

https://www.bilibili.com/video/BV1f34y1e7EK/?spm_id_from=333.788.recommend_more_video.1&vd_source=32f9de072b771f1cd307ca15ecf84087 https://www.bilibili.com/video/BV1Gs4y157BU/?vd_source=32f9de072b771f1cd307ca15ecf84087