3dv入门—NeRF

6 minute read

Published: February 10, 2024

在漫威的Snap卡牌游戏中，升级卡牌的方式是这样的，2D->打破边框->3D->动画….

NeRF的整体思路是像素坐标系—->相机坐标系—->世界坐标系

NeRF的贡献总结

贡献1：提出了5d的神经辐射场，利用5d的信息加入了$\phi$和$\theta$两个
贡献2: 体渲染技术，做可微渲染
贡献3: 使用位置编码将5维的输入转换到更高维的空间中去

一些基础的图像学知识和光学知识

什么是渲染，什么又是体渲染？

渲染是图形学中的核心概念。
计算机图形学：让计算机模拟出一个真实的世界
渲染：则是把这个虚拟出来的世界投影成图像，正如自然界中的各种光线经过碰撞后，投影到我们视网膜上的样子

体渲染属于整个渲染技术的一个分支，它的目的主要是为了解决云、烟、果冻这类非刚性物体的渲染建模，可以简单理解为是为了处理密度较小的非固体的渲染，如果看下文还可以发现这可以推广到固体的渲染中

为了建模这种非刚性的物体的渲染，体渲染选择把气体能物质抽象成一团飘忽不定的粒子群。而光线在穿过这类物体时候，就是光子与粒子发生碰撞的过程。

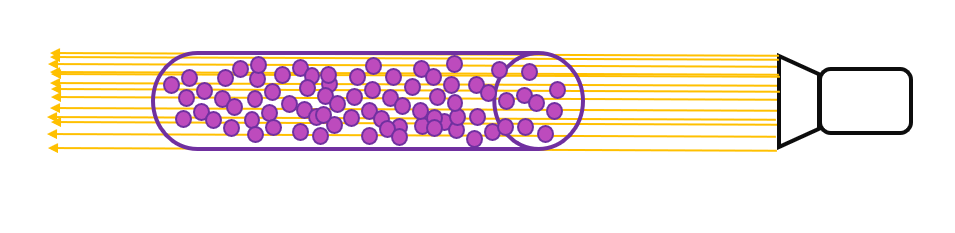
体渲染建模示意图

光沿直线方向穿过一堆粒子 (粉色部分)，如果能计算出每根光线从最开始发射，到最终打到成像平面上的辐射强度，我们就可以渲染出投影图像。而体渲染要做的，就是对这个过程进行建模。为了简化计算，我们就假设光子只跟它附近的粒子发生作用，这个范围就是图中圆柱体大小的区间。

体渲染把光子与粒子发生作用的过程，进一步细化为四种类型：

吸收 (absorption)：光子被粒子吸收，会导致入射光的辐射强度减弱；
放射 (emission)：粒子本身可能发光，比如气体加热到一定程度就会离子化，变成发光的「火焰」。这会进一步增大辐射强度；
外散射 (out-scattering)：光子在撞击到粒子后，可能会发生弹射，导致方向发生偏移，会减弱入射光强度；
内散射 (in-scattering)：其他方向的光子在撞到粒子后，可能和当前方向上的光子重合，从而增强当前光路上的辐射强度。

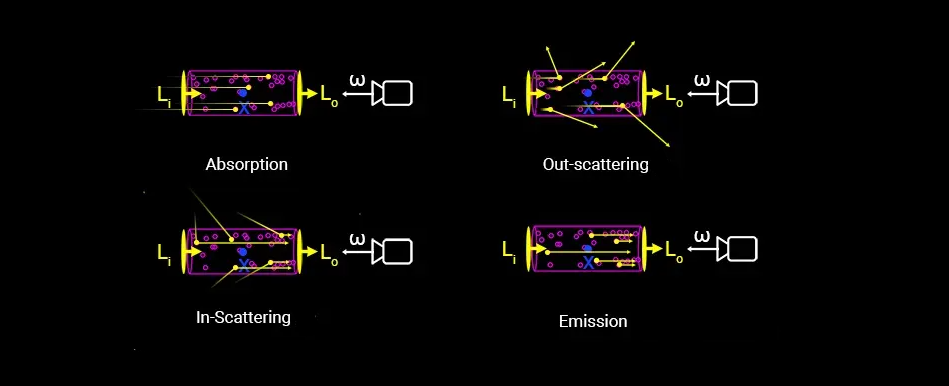
四种情况的示意图

上图中，$L_{i}$为入射的光，而$L_{o}$为出射的光

出射光与入射光之间的变化量，可以表示为这四个过程的叠加：

\[L_o-L_i=dL(x,w)=emission+inscattering-outscattering-absorption\]

接下来我们对这四个过程展开分析：

关于吸收

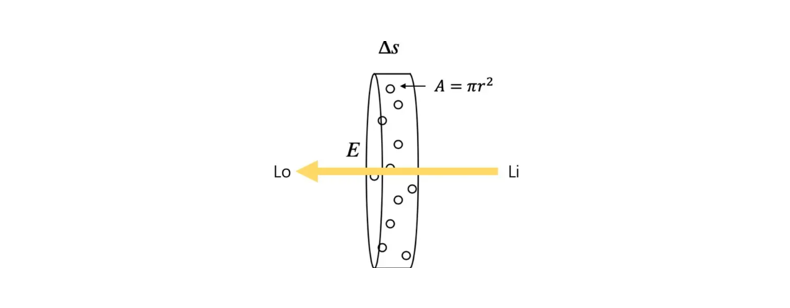
假设粒子都是半径为$r$的球体，那么每个粒子的投影面积是$A=\pi r^2$(也就是每个粒子对光线的遮挡面积),假设圆柱体中粒子的密度为$\rho$,圆柱体的底面积为$E$

当圆柱体足够薄 (薄到跟粒子一样厚) 的时候，可以认为粒子之间不会互相重叠 (也就是粒子都平铺在圆柱体一个横截面上)。

假定这个厚度是$\Delta s$,那么在这个厚度内圆柱体体积为$E\Delta s$,粒子的总数为$\rho E \Delta s$

这些粒子的遮挡的面积为$\rho E \Delta s A$,占整个底面积的比例为$\frac{\rho E \Delta s A}{E}$,也即，当一束光通过这个圆柱体的时候，有$\rho \Delta s A$的概率会被遮挡。

换句话说，如果我们在圆柱体的一端发射无数光线 (假设都朝相同的方向)，在另一端接收，会发现有些光线安然通过，有些则被粒子遮挡 (吸收)。但可以确定的是，这些接受到的光线总强度，相比入射光线总强度而言，会有$\rho \Delta s A$比例的衰减，即出射光的强度均值是入射光的$\rho \Delta s A$倍

数学上可以表示为：

\[I_o-I_i=\Delta I=-\rho(s)AI(s)\Delta s\]

关于放射

高中物理的某一章节一定讲过，“粒子本身是会发光的”，这里的发光就是指粒子本身的放射。

这里我们假设一个粒子发射一束光的辐射强度为$I_{e}$,那么按照前文的描述，在粒子足够薄的情况下，粒子总数是$\rho AE\Delta s$,那么其总的发光强度为$I_e \rho AE\Delta s$。

如果我们在圆柱体一端去接收粒子们放射的光线，会发现有时候能接收到，有时候刚好接收点所在的光路上没有粒子，就接收不到。能接收到光线的概率为$\rho AE\Delta s/E=\rho A\Delta s$,其接收到的平均的光强度为$I_e\rho A\Delta s$。

关于外散射

粒子除了吸收光子，也可能会弹射光子，这个过程称为外散射，即光子被弹射出原本的光路，导致光线强度减弱，这个过程的具体影响之后再说(目前情况太复杂了，已经是纯纯的物理建模了)。

体渲染公式引入

在了解了上述的基本知识后，我们终于可以引入体渲染公式了

\[C(\mathbf{r})=\int_{t_n}^{t_f}T(t)\sigma(\mathbf{r}(t))\mathbf{c}(\mathbf{r}(t),\mathbf{d})dt,\mathrm{~where~}T(t)=\exp\!\left(-\int_{t_n}^t\sigma(\mathbf{r}(s))ds\right)\]

体渲染公式，是一个本来就存在的东西，其中$\mathbf{r}(t)=\mathbf{o}+t\mathbf{d}$

\[T\left(t\right)=\exp\left(-\int_{t_n}^{t}\sigma\left(\mathbf{r}\left(s\right)\right)\mathrm{d}s\right)\]

这里$T(t)$是指光随着距离衰减的程度，指的是，到达一个点之后，光强还剩下多少，同时这里的$\sigma$为粒子的密度大小，与颜色$c(.)$一样，他们都是在在面NeRF可以学习出来的值。

NeRF中所用的Trick

Trick1-位置编码

位置编码运用了低频的特性，给神经网络输入一个低频的东西，输出也会是一个比较低频的东西；对于神经网络来说，输入就是这个点的x,y,z坐标还有这个点的方向角，例如$(0,0,0)$和$(0,10,0)$之间的差距其实就是低频的，通过神经网络输出的结果也是低频的，也就是差距不会很大，渲染出来的颜色比较平滑，相邻的颜色差距很小；

\[\gamma(p)^{\mathfrak{k}}=\left(\sin(2^0\pi p),\cos(2^0\pi p),\cdots,\sin(2^{L-1}\pi p),\cos(2^{L-1}\pi p)^{^{\prime}}\right)\]

利用这种位置编码，我们就可以把输入变成一个高频的东西，如果是原来非常相邻的两个点，经过这样的一个表示就会变得非常不一样。此处的$p$指的是$(x,y,z)$，一般只对空间位置进行，而不会对方向角进行，因此被成为空间位置编码。

Trick2-分级采样(View Dependence)

解决问题：点的采样是一个均匀采样，均匀采样会导致一个问题，在$t_{near}$到$t_{far}$的距离中，有很多点是空气点，采样出来的密度就是0，而在体渲染公式中是一累乘的连续形式，而这样的均匀采样又会不可避免的采样到这种空气地方。

作者的解决方案：分两步走，首先用等间隔采样(均匀采样方式)去训练得到一个NeRF，然后NeRF可以在这条光线上绘制出其$\sigma$的变化曲线出来，得到这个变化曲线之后，就可以按照密度去采样，可以在$\sigma$比较小的地方，用很小的采样点，在$\sigma$比较大的地方，用较多的采样点，去做比较精细的采样。在代码中则是一个是粗网络，一个是细网络。

相机成像知识补充

世界坐标系与虚拟坐标系

世界坐标系是我们规定好的一个点，而相机坐标系是在世界坐标系中随机规划好的一个点；同一个点，这里规定世界坐标系里表示为$(X_w,Y_w,Z_w,1)$,规定在相机坐标系里表示是$(X_c,Y_c,Z_c,1)$,世界坐标到相机坐标的变换可以使用齐次坐标的矩阵形式表示为：

\[\begin{bmatrix}X_c\\Y_c\\Z_c\\1\end{bmatrix}=\begin{bmatrix}R_{11}&R_{12}&R_{13}&T_x\\R_{21}&R_{22}&R_{23}&T_y\\R_{31}&R_{32}&R_{33}&T_z\\0&0&0&1\end{bmatrix}\begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix}\]

其中的

\[\begin{bmatrix}R_{11}&R_{12}&R_{13}&T_x\\R_{21}&R_{22}&R_{23}&T_y\\R_{31}&R_{32}&R_{33}&T_z\\0&0&0&1\end{bmatrix}\]

这个4x4的矩阵为相机的外参数(相机的位置和相机的倾斜角度)，可以在外界获取，然后这个矩阵也是可逆的，代表我们可以利用世界坐标去求相机坐标。

关于相机成像的更详细的内容可以看这一篇blog

代码解析

粒子采集

射线的构造

# Ray helpers
def get_rays(H, W, K, c2w):
  """
  H:图片的高度
  W:图片的宽度
  K:相机的内参  其中K[0][2] = W//2,K[0][1] = H//2,K[1][1] = 焦距f
  c2w：转换矩阵（旋转+平移）
  """
    i, j = torch.meshgrid(torch.linspace(0, W-1, W), torch.linspace(0, H-1, H))  # pytorch's meshgrid has indexing='ij'
    i = i.t()
    j = j.t()
    dirs = torch.stack([(i-K[0][2])/K[0][0], -(j-K[1][2])/K[1][1], -torch.ones_like(i)], -1)
    # Rotate ray directions from camera frame to the world frame
    rays_d = torch.sum(dirs[..., np.newaxis, :] * c2w[:3,:3], -1)  # dot product, equals to: [c2w.dot(dir) for dir in dirs]
    # Translate camera frame's origin to the world frame. It is the origin of all rays.
    rays_o = c2w[:3,-1].expand(rays_d.shape)
    return rays_o, rays_d

这是用于得到射线的代码，目前其中i和j用于组合得到具体的坐标，（以从长度和宽度都为400为例子）其中的i是这样子的：

\[i=\begin{bmatrix} 0,1,2,...,399 \\ 0,1,2,...,399 \\\cdots\\ 0,1,2,...,399 \end{bmatrix}\]

而j是这样子的：

\[j=\begin{bmatrix} 0,0,0,...,0 \\ 1,1,1,...,1 \\\cdots\\ 399,399,399,...,399 \end{bmatrix}\]

根据前面得到的$r(t)=o+td$,我们可以得到rays_d就是每条射线的方向，而rays_o就是每条射线的原点，他们的形状都为的形状为[400,400,3]。

实际应用过程中图片的大小可能更大，我们做不到每次都使用全部的射线，因此这里创建射线时候往往是从一张图中已经创建的射线中去进行采样，（使用随机函数）

粒子的采集

对于图片上的某一个像素(u,v)，我们认为其像素最终值是沿着某一射线上的无数个发光点的和，该射线可以表示为$r(t) = o + td$,其中$o$为射线原点，$d$为方向，$t$为距离。因此我们选择从射线上去进行采样，采样的具体方法是这样的：

设置$near$为2，$far$为6，选择在$near$和$far$之间进行均匀地采样:

near, far = near * torch.ones_like(rays_d[...,:1]), far * torch.ones_like(rays_d[...,:1])

N_rays = ray_batch.shape[0]  # 之前已经将rays_o和rays_d还有其他打包成了ray_batch
rays_o, rays_d = ray_batch[:,0:3], ray_batch[:,3:6] # [N_rays, 3] each
viewdirs = ray_batch[:,-3:] if ray_batch.shape[-1] > 8 else None   # 这里可以忽略这个
bounds = torch.reshape(ray_batch[...,6:8], [-1,1,2])
near, far = bounds[...,0], bounds[...,1] # 

t_vals = torch.linspace(0., 1., steps=N_samples)

if not lindisp:
    z_vals = near * (1.-t_vals) + far * (t_vals)
else:
    z_vals = 1./(1./near * (1.-t_vals) + 1./far * (t_vals))

z_vals = z_vals.expand([N_rays, N_samples])

if perturb > 0.:
    # get intervals between samples
    mids = .5 * (z_vals[...,1:] + z_vals[...,:-1])
    upper = torch.cat([mids, z_vals[...,-1:]], -1)
    lower = torch.cat([z_vals[...,:1], mids], -1)
    # stratified samples in those intervals
    t_rand = torch.rand(z_vals.shape)

    # Pytest, overwrite u with numpy's fixed random numbers
    if pytest:
        np.random.seed(0)
        t_rand = np.random.rand(*list(z_vals.shape))
        t_rand = torch.Tensor(t_rand)

    z_vals = lower + (upper - lower) * t_rand

# r(t) = o + td
pts = rays_o[...,None,:] + rays_d[...,None,:] * z_vals[...,:,None] # [N_rays, N_samples, 3]

关于z_vals，也即根据采样间隔采样后的点的位置，这里提供了两种方式，一种是绝对的线性采样，另一种是非线性采样。if perturb > 0.:这里是开始根据选择是否有添加扰动。最终，例如我们要有1024条射线，然后每条射线设置采样64个点，最终得到的形状为$[1024,64,3]$，最终也即采样到了1024*64个点。

根据这两段代码，我们大概已经明白了如何从图片和相机位姿中计算射线以及如何从射线上采样粒子，但是此时还有一个盲点，我们已经得到的是每个点的$(x,y,z)$的三个坐标;但是我们之前提到过，还有$(\theta,\phi)$这两个参数，他们代表的是粒子在三D表示时候的仰角和方位角，但是在rays_d已经使用三个坐标将方向这个概念表达清楚，因此这里就直接采用的rays_d表达的方法，所以其实输入还是一个六维的输入。

raw = network_query_fn(pts, viewdirs, network_fn)
rgb_map, disp_map, acc_map, weights, depth_map = raw2outputs(raw, z_vals, rays_d, raw_noise_std, white_bkgd, pytest=pytest)

这段代码中的pts就是粒子的$x,y,z$三坐标，然后viewdirs则是粒子的方向表示，就是之前的rays_d。

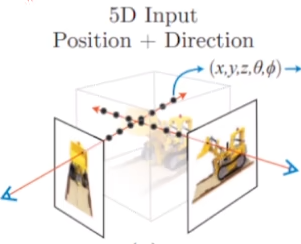
NeRF输入的示意图

至此，这也与NeRF论文中输入的示意图完美地呼应了起来。

网络的输入

根据NeRF原本论文中提供的网络框图，我们发现其网络的输入竟然是达到了60维度，但是我们之前得到的坐标原点+方位角也不过是3+3=6维度，为什么是60维度呢？以及在该张图片的右下角，还有一个24维，不慌，让我们来稍微细致的剖析一下。

网络结构

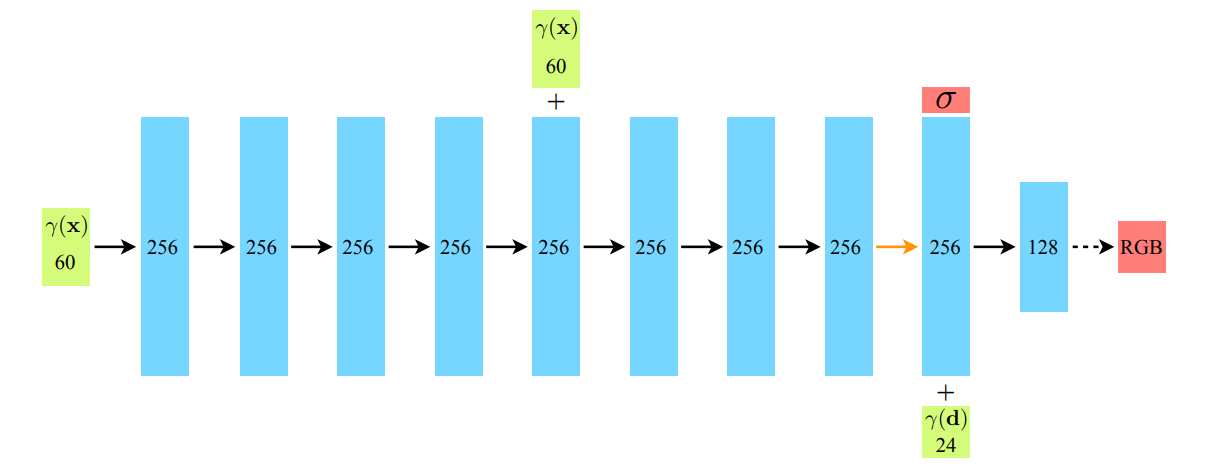
这就要涉及到我们之前所说的“NeRF中所用的trick”，我们不妨再重述一遍，因为作者在实验中发现，如果只输入3d的位置和3d的方向信息，这样会让建模的信息丢失(参考上文中神经网络的低频特性)，那么如何在输入时候也加入高频的信息呢，NeRF采用的是与Transformer结构一样的在加入位置编码的操作：

\[\gamma(p)=(\sin(2^{0}\pi p),\cos(2^{0}\pi p),\ldots,\sin(2^{L-1}),\cos(2^{L-1}\pi p))\]

对于空间坐标$(x,y,z)$，我们将L设置为10，那么$\gamma(x)$的维度就来到了60维(其中的$(x,y,z)$均有20个)，对于视角坐标$d$，选择将L设置为4，那么$\gamma(d)$的维度就来到了24维（不过实际的代码中，是使用位置编码之后的60维与原来的原始3维度信息进行拼接得到的才是真正输入的信息63维。）

这里有一个很重要的细节，我们可以发现在将视角坐标信息输入到网络之前，就已经输出了$\sigma$的密度信息，是密度信息$\sigma$再加上视角坐标信息，最后才输出的是颜色信息。也即颜色跟视角有关，但是密度信息跟视角是无关的。

NeRF网络的结构

可以看到NeRF的网络基本上就全是全连接层，红色框框的位置是第二次加入坐标信息和最后加入视角坐标信息的地方。

NeRF的Loss是什么？

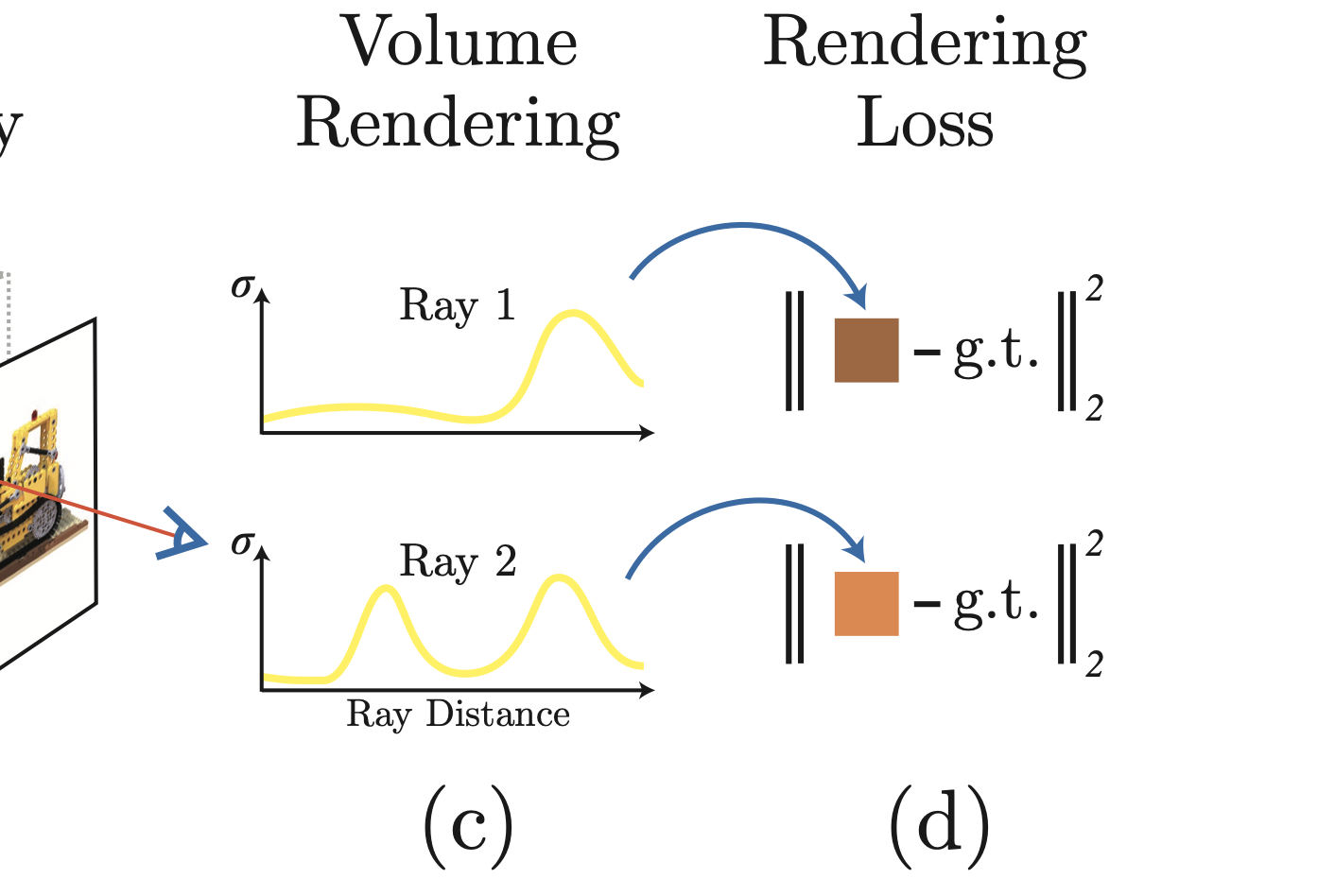
我们之前说到，将一条射线上所有的采样点的进行叠加，最终预测得到该点处颜色$\hat{C}(r)$的值，因此在NeRF中的真值GT为真实图片对应像素的RGB值$C(r)$，我们想要的无非是输出与原来颜色，形状一样的图片，因此这里的损失可以简单地使用MSE来进行计算。

\[L=\sum_{r\in R}| | \hat{C}(r)-C(r) | |_{2}^{2}\]

其中的$R$是每个batch的射线的数量。

颜色的叠加–体渲染的真正用途！

我们一直在讲将一条射线上所有的采样点进行叠加(粒子求和)这一概念，但是是如何叠加的呢，粒子又是如何求和的呢？这就要用到我们在前文中花费了大篇幅写的体渲染公式的知识了。

为了便于理解，我们先写下连续的积分公式：

\[\hat{C(s)}=\int_0^{+\infty}T(s)\sigma(s)C(s)ds\]

其中的$\sigma(s)$就是密度，而$C(s)$就是指的颜色，也就是这样通过每一点处的颜色的累加进行；

符合直觉

但是有一个更符合直觉的事情，如果在一条路径上，有一个点特别特别的亮，那么毫无疑问，他会遮蔽掉后面的光，对于后面那些亮度微弱的光，甚至就不会显示在最终的颜色上了，因此我们还要引入一个$T(s)$，用于表述在s点之前，光线没有被阻碍的概率是多少，如果是被阻拦了，那么$T(s)$就为0，也就不用管后面的事情了,$T(s)$的计算方式为：

\[T(s)=e^{-\int_0^s\sigma(t)dt}\]

对于这里的符合直觉的$T(s)$，我们还是有必要将其证明下为好，这里是将之前提到的密度$\sigma(s)$建模为可能被阻拦的概率：

原理刨析

更为详细彻底的推导可以参考这一篇NeRF入门之体渲染 (Volume Rendering)，这里简单推导下$T(s)$的来源

这里我们针对一条光线上的某一段$ds$，那么假设我们已知$T(s)$,那么$\sigma(s)ds$就是在这一段上被阻挡得概率:

\[\begin{aligned} &T(s+ds)=T(s)[1-\sigma(s)ds] \\ &T(s+ds)=T(s)-T(s)\sigma(s)ds \\ &T(s+ds)-T(s)=- T(s)\sigma(s)ds \\ &dT(s)=- T(s)\sigma(s)ds \\ &\frac{dT(s)}{T(s)}=- \sigma(s)ds \end{aligned}\]

微分方程知识补充

体渲染公式是一种很典型的常微分方程 (ordinary differential equation, ODE)。所谓常微分方程，指的是方程中包括函数$y(x)$以及导数$y’(x)$，并且只包含一个变量$x$ 。如果只包含一阶导，则称为一阶常微分方程。

为了能搞好理解下面的推导,这里补充一些微分方程的知识(~~复习高数~~)

线性，齐次，系数为常数的

最简单的一类常微分方程是这样$y^{\prime}(x)+\alpha y(x)=0$

求解过程为：

\[\begin{aligned} \frac{y^{\prime}}{y}& =-\alpha \\ \int\frac{y^{\prime}}{y}dx& =-\int\alpha dx \\ \ln y+C& =-\alpha x \\ y(x)& =Ce^{-\alpha x} \end{aligned}\]

线性，齐次

接下来升级一下，把常数替换为函数：$y’(x)+p(x)y(x)=0$

求解过程：

\[\begin{aligned} \frac{y^{\prime}}{y}& =-p \\ \int\frac{y^{\prime}}{y}dx& =-\int pdx \\ \ln y& =-\int pdx+C \\ y(x)& =Ce^{\int p(x)dx} \end{aligned}\]

看完上面的这些知识，我们可以很自然地对$\frac{dT(s)}{T(s)}=-\sigma(s)ds$进行求解：

\[\begin{aligned} \int_0^t\frac{dT(s)}{T(s)}& =\int_0^t-\sigma(s)ds \\ \int_0^t\frac{1}{T(s)}dT(s)& =\int_0^t-\sigma(s)ds \\ \ln T(s)\big|_{0}^{t}& =\int_0^t-\sigma(s)ds \\ \ln T(t)-\ln T(0)& =\int_0^t-\sigma(s)ds \\ \ln T(t)& =\int_0^t-\sigma(s)ds \\ T(t)& =e^{\int_0^t-\sigma(s)ds} \end{aligned}\]

在上面的推导中，我们认为$T(0) = 1$，也即在0这个位置是没有任何东西阻挡得。

体渲染公式的离散化

我们将整个光路$[0,s]$划分为$N$个相等间距的区间：$N \times [t_{n},t_{n+1}]$。那么，只要能算出每个区间$[t_{n},t_{n+1}]$内的辐射强度$I(t_n\to t_{n+1})$ ，最后把这$N$个区间的辐射加起来，就可以得到最终的光线强度了。$N$越大，也即离散的程度越大，则越接近理论数值

体渲染公式的离散化

在前文中，我们给出了连续的体渲染公式，但是跟我们之前选择从一条射线上进行采样一样，我们没有办法在计算机中进行真正的连续的积分，因此，我们需要再次将符合直觉的连续的体渲染公式进行符合直觉的离散化。

在一段光线的$[0,s]$距离上，可以选择将光线划分为N个等间距的区间$[T_{n}\to T_{n+1}]$,在每一个区间上的颜色和密度都是固定的，这里先给出一个公式：

\[\hat{C}(r)=\sum_{i=1}^NT_i(1-e^{-\sigma_i\delta_i})c_i\]

其中$T_i=e^{-\sum_{j=1}^{i-1}\sigma_j\delta_j}$

这里我们反着来推导一下，最终的颜色呈现从所有的粒子变到了所有的光区贡献的光强进行累加$\hat{C}=\sum_{n=0}^NI(T_n\to T_{n+1})$,这里的$I(T_n\to T_{n+1})$就是经过了 $T_n$到$T_{n+1}$而没有被阻拦的概率 $\begin{aligned} I(T_{n}\rightarrow T_{n+1})& =\int_{t_{n}}^{t_{n+1}}T(t)\sigma_{n}C_{n}dt \\ &=\sigma_{n}C_{n}\int_{t_{n}}^{t_{n+1}}T(t)dt \\ &=\sigma_{n}C_{n}\int_{t_{n}}^{t_{n+1}}e^{-\int_{0}^{t}\sigma(s)ds}dt \\ &=\sigma_{n}C_{n}\int_{t_{n}}^{t_{n+1}}e^{-(\int_{0}^{t_{n}}\sigma(s)ds+\int_{t_{n}}^{t}\sigma(s)ds)}dt \\ &=\sigma_{n}C_{n}\int_{t_{n}}^{t_{n+1}}e^{-\int_{0}^{t_{n}}\sigma(s)ds}e^{-\int_{t_{n}}^{t}\sigma(s)ds}dt \\ &=\sigma_{n}C_{n}T(0\to t_{n})\int_{t_{n}}^{t_{n+1}}e^{-\int_{t_{n}}^{t}\sigma(s)ds}dt \end{aligned}$

代码运行

在下载好数据集之后，我们运行命令python run_nerf.py --config configs/fern.txt，如果看到下面的输出，代表正常运行：

(CMS2) dell@dell-Precision-7920-Tower:/mnt/data/CMS/OSR/code2/111/nerf-pytorch$ python run_nerf.py --config configs/fern.txt
/home/dell/anaconda3/envs/CMS2/lib/python3.9/site-packages/torch/__init__.py:614: UserWarning: torch.set_default_tensor_type() is deprecated as of PyTorch 2.1, please use torch.set_default_dtype() and torch.set_default_device() as alternatives. (Triggered internally at ../torch/csrc/tensor/python_tensor.cpp:451.)
  _C._set_default_tensor_type(t)
Loaded image data (378, 504, 3, 20) [378.         504.         407.56579161]
Loaded ./data/nerf_llff_data/fern 16.985296178676084 80.00209740336334
recentered (3, 5)
[[ 1.0000000e+00  0.0000000e+00  0.0000000e+00  1.4901161e-09]
 [ 0.0000000e+00  1.0000000e+00 -1.8730975e-09 -9.6857544e-09]
 [-0.0000000e+00  1.8730975e-09  1.0000000e+00  0.0000000e+00]]
Data:
(20, 3, 5) (20, 378, 504, 3) (20, 2)
HOLDOUT view is 12
Loaded llff (20, 378, 504, 3) (120, 3, 5) [378.     504.     407.5658] ./data/nerf_llff_data/fern
Auto LLFF holdout, 8
DEFINING BOUNDS
NEAR FAR 0.0 1.0
Found ckpts []
get rays
done, concats
shuffle rays
done
Begin
TRAIN views are [ 1  2  3  4  5  6  7  9 10 11 12 13 14 15 17 18 19]
TEST views are [ 0  8 16]
VAL views are [ 0  8 16]

同时，我们来看一下在GTX 4090上的显存占用情况：

+---------------------------------------------------------------------------------------+
| NVIDIA-SMI 535.161.07             Driver Version: 535.161.07   CUDA Version: 12.2     |
|-----------------------------------------+----------------------+----------------------+
| GPU  Name                 Persistence-M | Bus-Id        Disp.A | Volatile Uncorr. ECC |
| Fan  Temp   Perf          Pwr:Usage/Cap |         Memory-Usage | GPU-Util  Compute M. |
|                                         |                      |               MIG M. |
|=========================================+======================+======================|
|   0  NVIDIA GeForce RTX 4090        Off | 00000000:73:00.0  On |                  Off |
| 85%   64C    P2             300W / 450W |   3705MiB / 24564MiB |     72%      Default |
|                                         |                      |                  N/A |
+-----------------------------------------+----------------------+----------------------+
|   1  NVIDIA GeForce RTX 4090        Off | 00000000:A6:00.0 Off |                  Off |
| 48%   37C    P8              27W / 450W |     21MiB / 24564MiB |      0%      Default |
|                                         |                      |                  N/A |
+-----------------------------------------+----------------------+----------------------+
                                                                                         
+---------------------------------------------------------------------------------------+
| Processes:                                                                            |
|  GPU   GI   CI        PID   Type   Process name                            GPU Memory |
|        ID   ID                                                             Usage      |
|=======================================================================================|
|    0   N/A  N/A      1574      G   /usr/lib/xorg/Xorg                           35MiB |
|    0   N/A  N/A     58950      G   /usr/lib/xorg/Xorg                          156MiB |
|    0   N/A  N/A     59096      G   /usr/bin/gnome-shell                         75MiB |
|    0   N/A  N/A     59789      G   /usr/local/sunlogin/bin/sunloginclient       12MiB |
|    0   N/A  N/A     59876      G   /usr/lib/firefox/firefox                     14MiB |
|    0   N/A  N/A    214596      C   python                                     3364MiB |
|    1   N/A  N/A      1574      G   /usr/lib/xorg/Xorg                            4MiB |
|    1   N/A  N/A     58950      G   /usr/lib/xorg/Xorg                            4MiB |
+---------------------------------------------------------------------------------------+

可以看到在一张4090上只占用了不超过4个G的显存，总体还是十分友好的。

读取数据时，打印其中的命令行参数结果为：

Namespace(config='configs/fern.txt', expname='fern_test', basedir='./logs', datadir='./data/nerf_llff_data/fern', netdepth=8, netwidth=256, netdepth_fine=8, netwidth_fine=256, N_rand=1024, lrate=0.0005, lrate_decay=250, chunk=32768, netchunk=65536, no_batching=False, no_reload=False, ft_path=None, N_samples=64, N_importance=64, perturb=1.0, use_viewdirs=True, i_embed=0, multires=10, multires_views=4, raw_noise_std=1.0, render_only=False, render_test=False, render_factor=0, precrop_iters=0, precrop_frac=0.5, dataset_type='llff', testskip=8, shape='greek', white_bkgd=False, half_res=False, factor=8, no_ndc=False, lindisp=False, spherify=False, llffhold=8, i_print=100, i_img=500, i_weights=10000, i_testset=50000, i_video=50000)

“使用”NeRF

学习他，理解他，使用它

我拍摄了一组关于Mr.misses(没错，就是瑞克与莫蒂里的那个万能小人)的照片(使用辣鸡相机素质的meizu20进行拍摄)，手机拍摄时候需要注意一点，就是在相机里调整到固定的焦段，然后再进行拍摄。

手机拍摄照片

然后按照网上的教程(有很多，这里不列举了)，大致的流程都是：导入colmap–>得到位姿信息–>输入NeRF–>渲染得到最终效果

最终效果展示

可以看到重建效果有，但是前一半时间的关注点似乎是错了，后半段视频的效果还挺不错，有空重新拍个别的试一试效果。

参考

Neural Radiance Fields 我起初心向明月 (zjwfufu.github.io)

NeRF入门之体渲染 (Volume Rendering) - 知乎 (zhihu.com)

NeRF数学公式从零推导，物理背景很重要

Twitter Facebook LinkedIn

Cai-Mingshuo

3dv入门—NeRF

NeRF的贡献总结

一些基础的图像学知识和光学知识

什么是渲染，什么又是体渲染？

关于吸收

关于放射

关于外散射

体渲染公式引入

NeRF中所用的Trick

Trick1-位置编码

Trick2-分级采样(View Dependence)

相机成像知识补充

代码解析

粒子采集

射线的构造

粒子的采集

网络的输入

NeRF的Loss是什么？

颜色的叠加–体渲染的真正用途！

微分方程知识补充

体渲染公式的离散化

体渲染公式的离散化

代码运行

“使用”NeRF

最终效果展示

参考

高数知识点复习

一些数字图像处理知识

Diffusion入门知识4—彻底搞懂扩散模型

Pytorch进阶之那些基础但重要的知识点二