Diffusion入门知识2—熟悉VAE
Published:
如果你跟VAE很熟,那你一定熟悉变分下界的推导吧
回顾
在Diffusion入门知识1中,我们简单了的了解了从AE到VAE的过程,了解到VAE的损失函数,其简洁的形式可以表示为
\[loss=MSE(X,X^{\prime})+KL(N(\mu_{1}, \sigma_{1}^{2}), N(0,1))\]其中的$MSE(X,X^{\prime})$是就是解码器解码得到的向量和输入向量之间的差距,或者说是重构的损失(reconstruct loss),$KL(N(\mu_{1}, \sigma_{1}^{2}), N(0,1))$则是为了使得编码器生成的隐变量$z$更贴近于正态分布。
本文一下两个角度引出
角度1—为什么要加入KL散度
reconstruct loss计算的是解码器解码得到的向量和输入向量之间的MSE loss,这一项比较好理解,就是反映出vae生成的结果和输入之间的差异,对应的目标是使vae生成的结果和输入尽可能相似,具体的原理基本类似于最小二乘拟合的原理来衡量误差
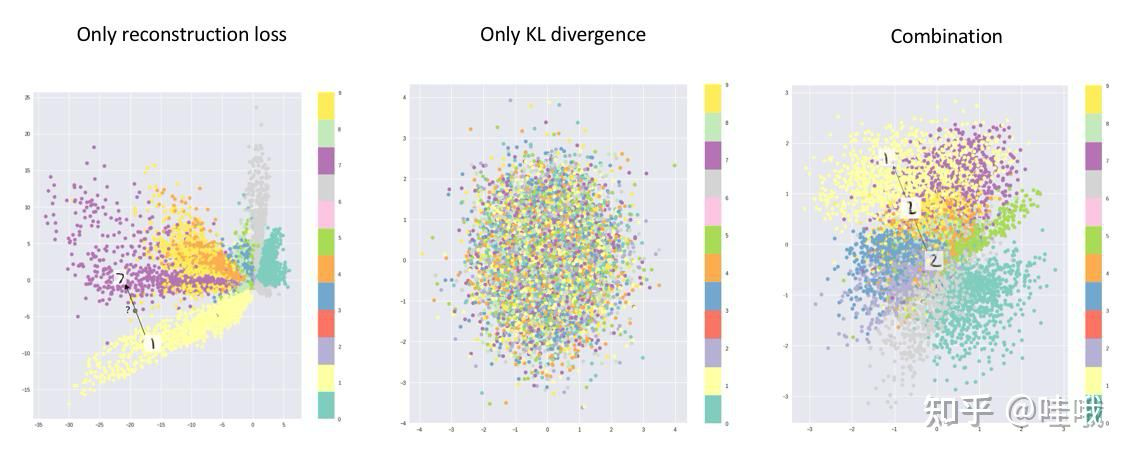
相较于MES loss的直观,kl散度正则项的理解就抽象一些了。从损失函数直观来看,是使得编码器生成的隐变量尽可能符合标准正态分布。 很直接的一种方法是让我们看看如果我们把reconstruct loss去掉,单单留下kl loss项会导致vae的编码空间变成什么样。这是我在网上找到的一张图片,中间显示的就是只采用kl散度训练后隐空间中的隐变量的分布。所有的输入向量均会被无差别地编码成标准正态分布。
角度2—加入KL散度是为了符合正态分布,那为什么要符合正态分布呢?
我之前疑惑的是为什么要符合正态的分布呢,这是我一直疑惑的点,为什么要引入这里的$\mu$和$\sigma^2$这里我主要参考这一篇给出的相应解释(插图也是来自这一篇,但我确实感觉这一篇讲的很好);
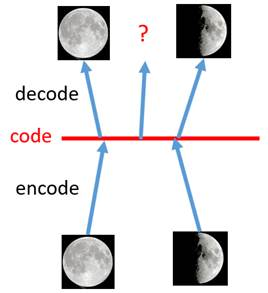
如下图所示,在编码的过程中,隐变量可以根据解码的数据编码出全圆月图和半圆月图,但是作为一个合格的生成模型,我们期望的是其可以生成3/4月亮或者1/4的月亮。
解决这个问题的一个思路是引入噪声,是的原有的图片的编码区域编码一些,也即从一对一变到一对多的情况,使得图片的编码区域可以变大,如下图所示使得其中的空白编码点被掩盖掉:
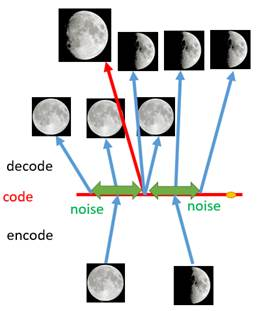
这种情况下,如果给图片编码时候加入一点噪音,那么每张图片的编码点会出现在绿色箭头的范围内(噪音就是绿色范围对应的地方),因此解码器在训练时候会把绿色范围内的点可以还原成这个绿色范围对应的原始图片。
而在两个绿色范围的交界处,也即中间地带,此处参杂了两种噪声,就很比较有可能产生我们想要的3/4月的形态。 但是这样还有一个问题,大家需要注意到图片中标注黄色的地方,是仍然没有被覆盖到的,也即仍然是个失真的点;
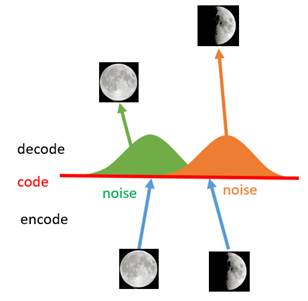
这种情况下的一个解决思路是把噪声无限拉长,“使得对于每一个样本,它的编码会覆盖整个编码空间,不过我们得保证,在原编码附近编码的概率最高,离原编码点越远,编码概率越低”,如下图: 这就是我们一直理解的分布的概念
总结来看,这种操作最核心的思想是将编码器架构从离散转为连续,这也是变分编码器的精髓思想。
VAE的理论基础
在GMM高斯混合模型的学习中,我们可以了解到任何一个存在的数据的分布,可以看作是若干个高斯分布的叠加,在下图中,若干个蓝色高斯分布叠加形成黑色的原始数据,可以被证明出(但具体证明是啥我现在也想不起来):当叠加数量很多时(512个),此时误差就变得很小很小了
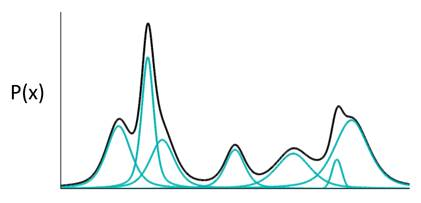
那么根据这个理论,我们在编码时,就可以将一组数据(黑色的线$p(x)$)抽象成许多个高斯分布的值
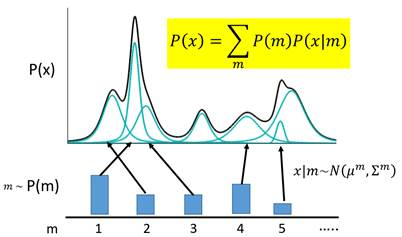
在标记黄色的公式中,$m$是对每个高斯分布的一个编号,每一个m对应一个小的高斯分布$N(\mu^{m},\Sigma^{m})$,此时$P(x)$就可以等价为所有这些高斯分布的叠加,这个公式是这样的:
\[P(x)=\sum_{m}P(m)P(x\vert m)\]其中$p(m)$是每个编号出现的的概率,在每个m中,x都有一个它对应的均值和误差值。
此时我们可以看到这仍然是个离散的表达形式,个人感觉这样已经是有了一定的拟合效果了,但是为何不想之前讲的那样,把这个变成离散的形式,从而更加的准备,也不会有空白值的情况出现,连续的形式是这样的:
\[P(x)=\int\limits_{z}P(z)P(x\vert z)dz\]其中有${z\sim N(0,1),x\vert z\sim N(\mu(z),\sigma(z))} (x\vert z指的是在z下的x分布)$,这个积分更加形象的样子可以参考下图,同时肯定这里为什么$z$一定要符合这个高斯的分布,很多地方都讲实际上并不一定要求这样
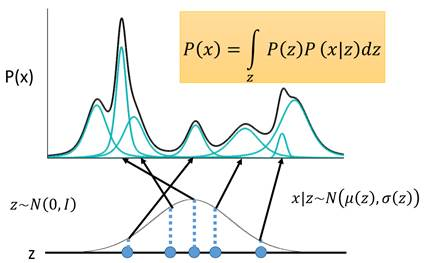
求解这个式子
已知$p(z)$是个0,1的正态分布,而$p(x\vert z)$是未知的,但是我们知道$x\vert z\sim N(\mu(z),\sigma(z))$,因此我们真正需要求解的是,$\mu(z)$和$\sigma(z)$这两个函数的表述式;但是$p(x)$,也就是原始图像的分布一般是很难得到的,因此VAE选择的是引入两个神经网络来帮助求解。
- Encoder的引入
第一个神经网络是Decoder,他求解的是$\mu$和$\sigma$这两个函数,这是我们求解$p(x\vert z)$的过程 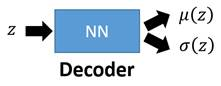
第二个神经网络叫做Encoder,它求解的结果是$q(z\vert x)$,$q$可以代表任何分布。

你可能好奇我为什么先引出Decoder再引出Encoder,这样做的为了体现Encoder主要是在辅助第一个Decoder求解$p(x\vert z)$,这是整个VAE中最为巧妙的概念。
我们最开始求解的目标式子是:$P(x)=\int\limits_{z}P(z)P(x\vert z)dz$
$p(x)$变得更大
很多地方对于这里的描述都是直接希望$p(x)$变得更大,但是我曾经迷惑了很久为什么要变得更大,算是进入了一个误区,因此我想稍微展开写一下:
- 隐秘的$\theta$
首先,需要明确此处VAE的目标是什么,是重建!我在学习VAE时候做的是使用VAE进行分类的任务,因此就造成了很大理解上的误区。
很多地方,包括本文之前一直都写的需要$p(x)$变得更大,但是可以参考wiki上的表述 \(p_\theta(x)=\int_zp_\theta(x,z)dz\)
\[p_\theta(x)=\int_zp_\theta(x\vert z)p_\theta(z)dz\]没错,大部分地方的表述都省略掉了$\theta$的概念,我们使用的VAE的目的是去重建出与原图一致或者符合原图分布的图像,在结构给出的情况下,我们要做的是去确定好模型的参数$\theta$
- 明白为什么要做最大化
在之前的概率论课程中,由于我只看重了刷题,因此每每看到最大似然估计是,我都会条件反射地去查wiki或者B站上的一个讲最大似然估计的视频Bilibili (这个小崔老师的视频我是看了不下十遍了),从而一直没有形成对最大似然估计直观上的理解,更不用说建立起最大似然估计与此处最大化$p_\theta(x)$的联想。
我每次查完最大似然估计,这都可以使用一句话来代替:首先,这是一个采样的过程,我们认为,概率越大的样本被采样到的可能性也是越大的,如果我们采样到了$X_{1},X_{2},…,X_{n}$,那么我们就认为这些样本对应的概率是最大的,因此,最大似然估计就是要计算出采样到 我们当前采样出来的点的情况 最大的模型参数$\theta$是怎样的,这样听起来有些拗口,但暂时我也找不到更好的表达了😅
这个时候我们可以回归到变分下界的推导上来,正如我们做题时取对数一样,我们把目标转化为$\max logP_\theta(x)$
\[log P_\theta(x) = \int_{z}P_\theta(x)P_\theta(x\vert z)dz\]根据条件概率公式可以得到
\[\int_{z}P_\theta(x)P_\theta(x\vert z) = \int_{z}q(z\vert x)log\left(\frac{P(z,x)}{P(z\vert x)}\right)dz\]这个时候再前文中我们一直说的$q(z\vert x)$
\[\int_{z}q(z\vert x)log\left(\frac{P(z,x)}{P(z\vert x)}\right)dz =\int_{z}q(z\vert x)log\left(\frac{P(z,x)}{q(z\vert x)}\frac{q(z\vert x)}{P(z\vert x)}\right)dz\]将这个log中的东西分开得到
\[\int_{z}q(z\vert x)log\left(\frac{P(z,x)}{q(z\vert x)}\frac{q(z\vert x)}{P(z\vert x)}\right)dz =\int_{z}q(z\vert x)log\left(\frac{P(z,x)}{q(z\vert x)}\right)dz+\int_{z}q(z\vert x)log\left(\frac{q\left(z\vert x\right)}{P(z\vert x)}\right)dz\]分开之后我们发现,右边这一项正好是大名鼎鼎的KL散度,于是我们得到了
\[log P_\theta(x) =\int_{z}q(z\vert x)\log\left(\frac{P(z,x)}{q(z\vert x)}\right)dz+KL\big(q(z\vert x)\vert P(z\vert x)\big)\]KL散度(也被称为相对熵),他的特点是会大于等于0(有待证明),因此我们可以得到
\[logP_\theta(x)\geq\int_{z}q(z\vert x)log\left(\frac{P_\theta(x\vert z)P_\theta(z)}{q(z\vert x)}\right)dz\]这里的$\int_{z}q(z\vert x)log\left(\frac{P_\theta(x,z)}{q(z\vert x)}\right)dz$根据概率论的知识,我们还可以进一步简化为 $E_{z\sim q(z\vert x)}[\log\frac{p(z,x)}{q(z\vert x)}]$ 这就是传说中的ELBO变分下界,我们将其标记为$L_{b}$,于是原式子变为:
\[logP_\theta(x)=L_{b}+KL(q(z\vert x)\vert \vert P(z\vert x))\]这个上面这一系列的变换我们能明白了,但是为什么要进行这样的变换呢?之前我们一直说的是我们要去最大化$P_\theta(x)$,而式5决定了当我们固定住$p(x\vert z)$时,$P_\theta(x)$的值也会随之固定,但当我们开始调节$q(z\vert x)$,让其不断变小,此时损失KL也会越变越小,而$L_b$则会不断变大;或者当我们把$q(z\vert x)$和$p(x\vert z)$调节到一样大小时,KL散度就完全为0了,$log P_\theta(x)$也彻底变成了$L_b$的样子;因此可以得到的一个重要结论是**不论$log P_\theta(x)$的怎样的,总存在一种情况$L_b$和$log P_\theta(x)$是相等的,因此我们直接将$log P_\theta(x)$和$L_b$等价起来,认为求解$\max logP_\theta(x)$就是求解$\max l_b$
然后,我们利用概率论的力量将$l_b$展开,便得到了我们平时常见很多的VAE的损失
\[\begin{gathered} \ {\mathcal L}_{b}=\int_{z}q(z|x)\log\left(\frac{P(z,x)}{q(z|x)}\right)dz \\ =\int_{z}q(z|x)log\left(\frac{P(x|z)P(z)}{q(z|x)}\right)dz \\ =\int_{z}q(z|x)log\left(\frac{P(z)}{q(z|x)}\right)dz+\int_{z}q(z|x)logP(x|z)dz \\ =-KL\big(q(z|x)||P(z)\big)+\int_{z}q(z|x)logP(x|z)dz \\ = -KL\big(q(z|x)||P(z)\big) + E_{q(z|x)}[\log P(x|z)] \end{gathered}\]总结
通过这次的记录,对VAE尤其是变分下界的推导熟悉了很多,但是推导的内容还是抄的这这一篇,期望以后可以自己完整地推一些独到的内容吧
